形式语言与自动机大作业

Overview

本次实验中需要实现命令行参数的校验、对于 PDA 和 TM 编码文件的解析、模拟输入字符串在 PDA 或 TM 上的执行（需要支持打印每一步执行的 verbose 模式），并且需要编写几个问题的 PDA 和 TM 编码

Misc

这个部分用于回忆一些背景知识…

C++

由于已经很久没写过 C++ 了，于是在这里记录一些浅显的要点

• .h 文件中写类的字段和成员函数的声明，以及其他工具函数的声明，具体的实现写在 .cpp 文件中

• pair 和 tuple 均不能直接作为 unordered_set 的元素和 unordered_map 的键，需要提供自定义的哈希函数

DPDA

本次实验要实现的是一个确定性下推自动机，其「确定性」的形式定义如下：

• $\forall q \in Q, a \in \Sigma \cup \{\epsilon\}, X \in \Gamma$，集合 $\delta(q, a, X)$ 最多有一个元素
• $\forall q \in Q, X \in \Gamma$，如果 $\delta(q, \epsilon, X) \neq \emptyset$，则 $\forall a \in \Sigma$，$\delta(q, a, X) = \emptyset$

本实验中的 DPDA 以到达终止状态（接受状态）来判定接受。注意对于 DPDA，以空栈接受和以终止状态接受其实是不等价的

TM

本次实验中要实现的是一个多带的确定性图灵机，它与普通的单带确定性图灵机最大的不同在于，有若干条纸带、每个纸带上都有一个读写头，但是状态是唯一的，每一步状态的迁移需要同时考虑到每个纸带上当前看到的字符

---

在调试平衡括号问题时遇到了一个现象，类似 fla ./case.pda () 的命令是会卡住的，原因是 () 在命令行中是有作用的。应该使用 fla ./case.pda "()"

Task

详见实验手册

Implementation

项目结构

project-2024/fla-project main*
❯ tree
.
├── args_parser.cpp
├── args_parser.h
├── main.cpp
├── msgs.h
├── pda.cpp
├── pda.h
├── tm.cpp
├── tm.h
├── utils.cpp
└── utils.h

1 directory, 10 files
VIM

main.cpp 为程序入口

args_parser 用于校验命令行参数，并存储文件名和输入字符串

msg.h 维护公共的输出信息

pda 定义了 PDA 类信息和相关逻辑

tm 定义了 TM 类信息和相关逻辑

util 定义了一些字符串处理的工具函数

命令行参数解析

Trivial.

PDA 的编码解析

• 使用正则表达式实现精细的匹配和校验，并且比较轻量，不用学习 Flex/Bison 等工具

  正则表达式做的只是「语法校验」，「输入字符串必须由输入符号集中的字符组成」这样的「语义校验」是随后的步骤

• 注释该如何处理

  将一行中 ; 及之后的字符全部忽略

PDA 的模拟执行

某一时刻，对于当前状态 $s$ 和当前栈顶符号 $a$，先看输入串是否还有待处理的字符

• 如果没有，则尝试是否有可行的空转移
  • 如果有，那么应用这个空转移，并进行下一步的处理
  • 如果没有，则停机
• 如果有，则尝试是否有对应的转移
  • 如果有，那么应用这个转移，并进行下一步的处理
  • 如果没有，则停机

在停机时，如果同时满足下面两条，则接受；否则拒绝

• 字符串处理完了
• 当前的状态是一个接受状态

verbose 模式

• 如果输入字符串不合法，则输出形如

  Input: 100A1A001
  ==================== ERR ====================
  error: 'A' was not declared in the set of input symbols
  Input: 100A1A001
  		  ^
  ==================== END ====================
  SUBUNIT

  只报告第一个出错字符

• 如果输入合法，那么开始模拟执行。在每轮循环的开始，输出形如

  Step  : 0
  State : 0
  Stack : 0 1 2 3 4 5 6
  Input : 1 0 0 1 0 0 1
  Head  : ^
  ---------------------------------------------
  ASCIIDOC

  注意 : 的对齐。其中 Stack 的最右边为栈底

  最终接受的输出是

  Result: true
  ==================== END ====================
  OXYGENE

  不接受时的输出是

  Result: false
  ==================== END ====================
  OXYGENE

TM 的编码解析

• 在编码解析阶段实现对于转移函数中旧符号组部分 * 的处理，基于笛卡尔积的思想暴力预处理出全部的可能。并且是利用闭包函数实现回溯的（理论上存在爆栈的可能，但是这不是在刷力扣

TM 的模拟执行

• 利用红黑树（map）模拟各条纸带，因为这样就不用花费精力考虑负数下标的情形了

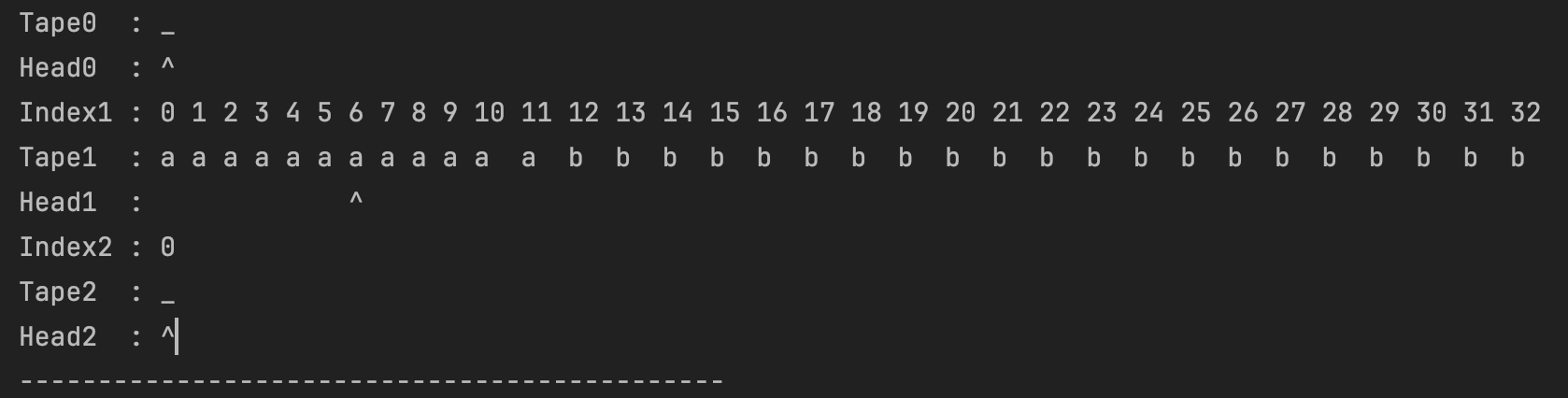
• verbose 模式下的输出有两点需要特别注意，以下面这个即时描述为例

  

  冒号左边的内容应该与最长的那行对齐，上图中是与 Index1 对齐；

  下标不止一位数时，对应的纸带上的符号应该与下标的最左边的数字保持对齐

• 由于在前一阶段预处理出了所有可行的转移函数，那么模拟执行时寻找转移函数就十分简单了

PDA 与 TM 的设计

用 DPDA 判断括号是否平衡

Trivial，括号平衡的算法题本身就可以用栈解决

用多带 DTM 实现一进制乘法

图灵机的输⼊为 $a^ib^j\ (i, j>0)$ 的形式，要求在图灵机停机时第 0 条纸带上的内容为 $c^{i \times j}$；若输⼊形式不符合要求，则在第一条纸带上输出 illegal_input

• 利用三条纸带，保证互不干扰。首先是把第 0 条纸带上的输入移到第 1 条纸带上
• 模拟乘法的本质。对于看到的每一个 $a$，遍历每一个 $b$，每看到一个 $b$，输出一个 $c$
• 输出 illegal_input 时，每一个字符都对应一个状态

用多带 DTM 判断完全平方数

判定如下语⾔： $L = \{1^p\ |\ p \text{ is a perfect square, }p \in \mathbb{N}^+\}$

若输⼊字符串在该语⾔中，则在第⼀条纸带上打印 true 后停机，否则打印 false 后停机

要利用到一个结论

一个完全平方数 $k^2$ 可以表示为前 $k$ 个奇数的和

$1+3+5+\dots+(2k-1)=(1+2k-1)*k/2=k²$

• 利用三条纸带，保证互不干扰。首先是把第 0 条纸带上的输入移到第 1 条纸带上
• 从小到大减去奇数，正好减到 0 就是完全平方数，否则不是
• 第 2 条纸带记录当前要减去的奇数，每次多加两个
• 注意不能接受空串

Reflection

• 编码图灵机解决问题十分新鲜，也很繁琐…
• 再也不想写 C++ 了…